5G 信道编码技术—Polar码

2023-04-17

本文代码均由MATLAB实现

引言

香农证明了，给定信噪比 $SNR$ 和带宽 $W$ Hz，在 AWGN 信道上能够进行可靠传输的最大速率为$𝑅 < 𝑊𝑙𝑜𝑔_2(1 + 𝑆𝑁𝑅)$。而极化码(Polar Codes)是 2008 年由 $E.Arikan$ 提出的一种新型信道编码，极化码基于信道极化进行设计，是第一种能够通过严格的数学方法证明达到信道容量的构造性编码方案（信道编码），并具有较低的编译码复杂度，当码长为N时，复杂度为 $O(NlogN)$。Polar码的核心思想就是信道极化理论， 它包括信道联合（Channel Combining）和信道分裂（Channel Splitting）两部分。当合并信道的数目趋于无穷大时，则会出现极化现象：一部分信道将趋于无噪信道，另外一部分则趋于全噪信道，这种现象就是信道极化。无噪信道的传输速率会达到信道容量$I(W)$，而全噪信道的传输速率趋于0。$Polar$码的编码策略正是应用了这种现象的特性，利用无噪信道传输用户的有用信息，全噪信道传输约定信息或不传信息。

信道极化基本原理

信道极化现象来自于信道联合（Channel Combining）和信道分裂（Channel Splitting）这两种信道操作，将N个BDMC信道 W 通过线性变换合并成$W_N$，然后再将$W_N$拆分为相关的信道 ，就是信道极化现象的具体实现过程。当信道容量$I(W)$在N趋于无穷时，一部分的信道容量接近1，而另一部分的信道容量趋于0，这样就可以在完美信道上发送信息比特，在噪声信道上发送休眠比特（一般为 0）。

在此之前，需要先了解用来衡量信道上的通信速率和可靠性的两种度量，即对称容量（Symmetric Capacity）和巴氏参数（Bhattacharyya Parameter）。

对称容量与巴氏参数

一个二进制输入离散无记忆信道（B-DMC）可表示为$W:X→Y$，$X$是输入符号集合，$Y$是输出符号集合，转移概率为 $W(y|x),x\in X,y\in Y$。

\[I(W) \triangleq \sum_{y \in Y} \sum_{x \in X} \frac{1}{2} W(y \mid x) \log \frac{W(y \mid x)}{\frac{1}{2} W(y \mid 0)+\frac{1}{2} W(y \mid 1)} \\ Z(W) \triangleq \sum_{y \in Y} \sqrt{W(y \mid 0) W(y \mid 1)}\]

$I(W)$是对信道速率的度量，信道W在等概率输入下时I(W)等于香农容量。

由信息论，信道容量公式如下，可知输入等概率情况下，$I(W)$有最大值即香农容量。

\[C=\max _{p\left(x_i\right)} I(X ; Y)=\max _{p\left(x_i\right)} \sum_i \sum_j p\left(x_i\right) p\left(y_j \mid x_i\right) \log \frac{p\left(y_j \mid x_i\right)}{\sum_i p\left(x_i\right) p\left(y_j \mid x_i\right)}\]

而Z(W)是信道W一次使用最大似然判决(ML)错误概率上限。$0\leq I(W),Z(W)\leq 1$，I(W)与Z(W)满足这样的关系：且仅当$Z(W)≈0$时，$I(W)≈1$；当且仅当$Z(W)≈1$时，$I(W)≈0$。

由二进制输入离散信道W在ML判决下错误率（寻找单点时间满足y在ML判决下结果非x的概率求和） $P_e^{ML}=\frac{1}{2}\sum_{y\in Y} min{W(y|0),W(y|1)}，P_e^{ML}\in [0,0.5]$，又有关系$ min{W(y|0),W(y|1)}\leq \sqrt{W(y|0)W(y|1)}$， 因此$P_e^{ML}\leq Z(W),Z(W)\in[0,1]$

常见信道

  • DMC（discrete memoryless channel ）离散无记忆信道：某时刻输出仅与当前输入有关

    转移概率矩阵

    $\textbf{Q}={q(y_j|x_k)}_{K*J} $

    对称DMC：转移概率矩阵的每一行都是第一行的置换，称该矩阵是输入对称的；如果转移概率矩阵的每一列都是第一列的置换，称该矩阵是输出对称的；如果输入、输出都对称，则称该DMC为对称的DMC信道。

  • BSC：二进制对称信道

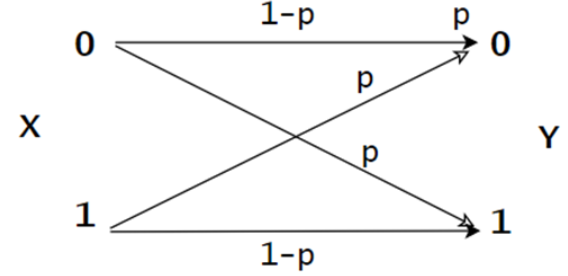
  • BEC：二进制删除信道

信道联合

将 N 个独立信道 W 通过变换使之变为一个具有“集体意义”的信道$W_N$，这里“集体意义”的产生来源于变换，是一个递归过程。联合B-DMC信道W的N个独立副本，通过递归方式产生一个向量信道$W_N:X^N\rightarrow Y^N$，其中N为2的幂次$N=2^n,n≥0$。这样通过递归 $N\rightarrow N/2\rightarrow \dots\rightarrow 2\rightarrow 1$ 就可以实现 N 个信道的合并。

  • n=0时，只有一个信道W，定义$W_1=W$。

  • n=1时，递归合并两个独立的$W_1$得到$W_2:X^2\rightarrow Y^2$

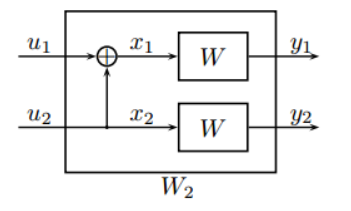
    状态转移概率为：

    \[W_2\left(y_1, y_2 \mid u_1, u_2\right)=W\left(y_1 \mid u_1 \oplus u_2\right) W\left(y_2 \mid u_2\right)\] \[x_1=u_1\oplus u_2,x_2=u_2\] \[\left[x_1, x_2\right] =\left[u_1, u_2\right]\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right] =\left[u_1, u_2\right] G_2\]

  • n=2时，有$W_4:X^4\rightarrow Y^4$，由两个$W_2$复合而成。

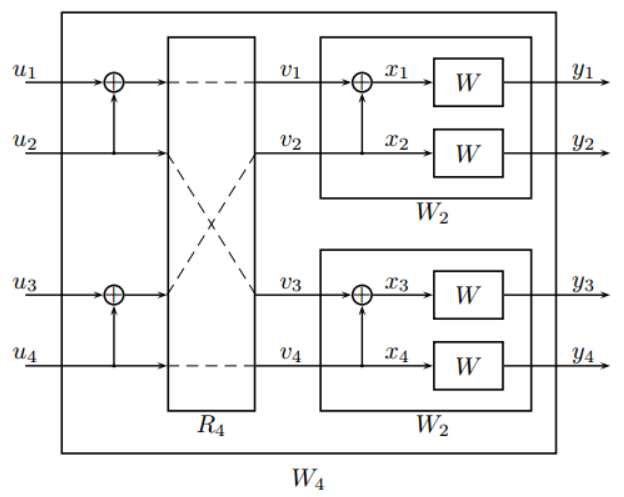
    \[\begin{aligned} W_4\left(y_1^4 \mid u_1^4\right) & =W_2\left(y_1^2 \mid u_1 \oplus u_2, u_3 \oplus u_4\right) W_2\left(y_3^4 \mid u_2, u_4\right) \\ & =W\left(y_1 \mid u_1 \oplus u_2 \oplus u_3 \oplus u_4\right) W\left(y_2 \mid u_3 \oplus u_4\right) W\left(y_3 \mid u_2 \oplus u_4\right) W\left(y_4 \mid u_4\right) \\ & =W^4\left(y_1^4 \mid u_1^4 G_4\right) \end{aligned}\] \[\left[x_1, x_2, x_3, x_4\right] =\left[u_1, u_2, u_3, u_4\right]\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] =\left[u_1, u_2, u_3, u_4\right] G_4\]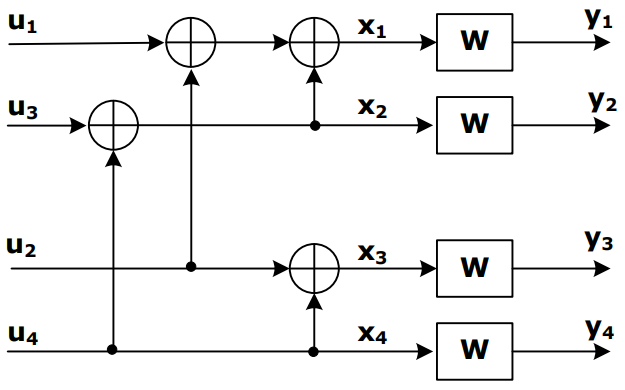

  • 递归结构一般形式如下：

    \[W_N\left(y_1^N \mid u_1^N\right)=W^N\left(y_1^N \mid u_1^N G_N\right) \quad y_1^N \in Y^N, u_1^N \in X^N\]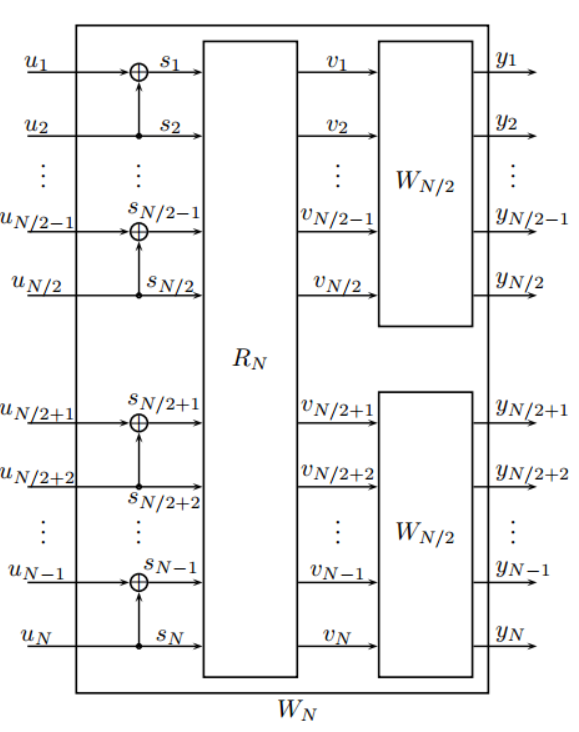

信道分裂

由于无法确知各个子信道的输入和输出是什么关系。这就需要对信道极化过程有一个微观的表达，这个微观表达是通过信道分裂过程来实现的。信道分裂使已经扭成一条粗线的联合信道又重新一条一条地展现在世人面前，就好比两条绳子打结（信道联合），然后再区分出两端谁是谁（信道分裂）。经过分裂的信道总是以单个的形式表达，如分裂子信道$W_N^{(i)}:X\rightarrow Y^N×X^{i−1}$，以及分裂子信道的转移概率 $W_N^{(i)}(y_1^N,u_1^{i−1}|u_i)$。

输入符号概率、输出符号概率和转移概率完整地定义了一种信道，下式即联合信道和分裂子信道的关系：

\[W_N^{(i)}\left(y_1^N, u_1^{i-1} \mid u_i\right) \triangleq \sum_{u_{i+1}^N \in X^{N-i}} \frac{1}{2^{N-1}} W_N\left(y_1^N \mid u_1^N\right)\]

但是不易求。而由信道联合递归图，整个信道极化过程恰好是一种递归形式。因此用两个递归式来计算各个分裂子信道的转移概率

\[\begin{gathered} W_N^{(2 i-1)}\left(\mathbf{y}_1^N, \mathbf{u}_1^{2 i-2} \mid u_{2 i-1}\right)=\frac{1}{2} \sum_{u_{2 i}} W_{N / 2}^{(i)}\left(\mathbf{y}_1^{N / 2}, \mathbf{u}_{1, o}^{2 i-2} \oplus \mathbf{u}_{1, e}^{2 i-2} \mid u_{2 i-1} \oplus u_{2 i}\right) W_{N / 2}^{(i)}\left(\mathbf{y}_{N / 2+1}^N, \mathbf{u}_{1, e}^{2 i-2} \mid u_{2 i}\right) \\ W_N^{(2 i)}\left(\mathbf{y}_1^N, \mathbf{u}_1^{2 i-2} \mid u_{2 i}\right)=\frac{1}{2} W_{N / 2}^{(i)}\left(\mathbf{y}_1^{N / 2}, \mathbf{u}_{1, o}^{2 i-2} \oplus \mathbf{u}_{1, e}^{2 i-2} \mid u_{2 i-1} \oplus u_{2 i}\right) W_{N / 2}^{(i)}\left(\mathbf{y}_{N / 2+1}^N, \mathbf{u}_{1, e}^{2 i-2} \mid u_{2 i}\right) \end{gathered}\]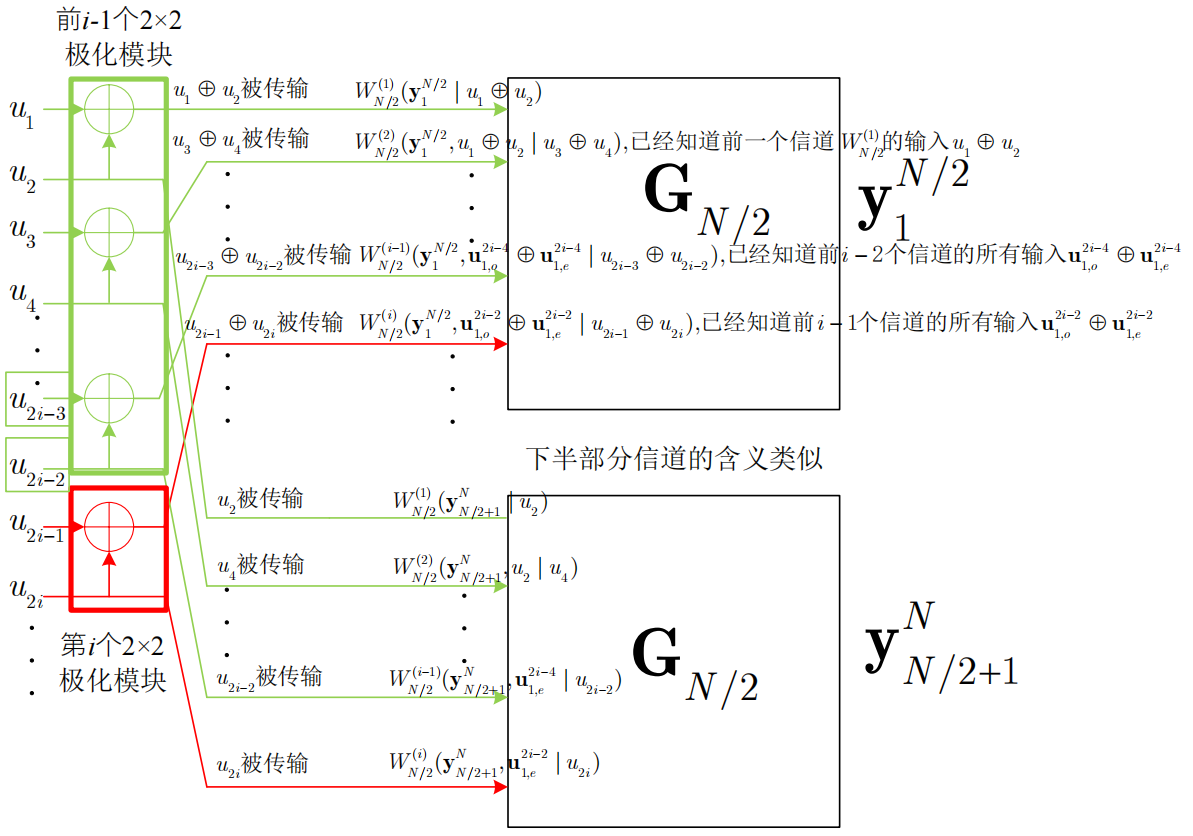

信道极化

  • 观察$W_2$信道，有

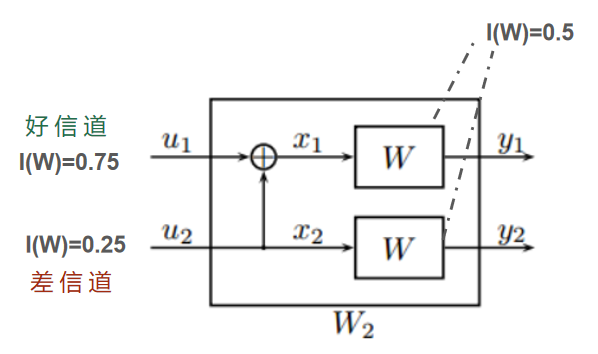
    $Y_1$ $Y_2$ $U_1$ $U_2$
    √ √ $Y_1\oplus Y_2\quad √$ $Y_2\quad √$
    × √ $?\oplus Y_2\quad ×$ $Y_2\quad √$
    √ × $Y_1\oplus ?\quad ×$ $U_1\oplus Y_1$
    × × $?\oplus ? \quad ×$ $? \quad ×$

    对于信道$U_1$，必须在$y_1$和$y_2$均接收正确的情况下才能得到正确的$U_1$，因此，信道容量$I_1(W)$就是$y_1,y_2$的信道容量的乘积$0.5*0.5$；

    如果$U_1$已知，则$U_2$只有在$y_1$和$y_2$均接收错误的情况下，才无法得到正确的信号。因此，$U_2$的信道容量$I_2(W)$为$20.5-0.50.5$。

  • 以此类推，在上述两种操作下，原本相同的N个W信道产生了极化现象，其中一部分信道的信道容量趋近于1，另一部分信道的信道容量趋近于0。

  • 利用MATLAB仿真观察极化现象如下（信道个数$N=2^{10}$，每个信道对称容量均为0.5）

    index = 10;%信道序号
n = 2.^(1:index);
W = zeros(n(10));%创建1024*1024的空矩阵
W(1, 1) = 0.5;%设置坐标为(1,1)的信道容量I(W)
for i = n
    for j = 1:i/2
        %前文已给出好信道和坏信道的信道容量计算方法
        W(i, 2 *j -1) = W(i/2, j)^2;%坏信道
        W(i, 2 *j) = 2 * W(i/2, j) - W(i/2, j)^2;%好信道
    end
end
%绘制信道极化现象
scatter(1:1024, W(1024, 1:1024), 'r.');
axis([0 1024 0 1]);
xlabel('信道序号i');ylabel('对称信道容量I(W)');

  • 从信道极化中可以隐约发现，信道合并与极化码的编码在形式上非常相似，而信道分裂与极化码的解码在形式上非常相似。根据对信道合并与分裂的观察，在极化码的仿真体系中：为了完成极化码编码，首要要构造生成矩阵；而信道分裂的特性隐约表明了极化码的译码应该采用串行译码的方式。此外，信道极化现象展示了极化码的宏观特性，经由分析极化现象中的特定参数，可以确定极化码编码过程中的信息位选取方案。

？差信道的用途？，如果只是把性能转移到好信道上，那总的性能提升在哪？？

差信道基本无需传输数据因此无需分配大带宽

极化编码

极化信道可靠性估计

  • 对于BEC信道，在Arikan论文中是通过计算巴氏参数估计信道可靠性。在信道极化基本原理中已知$Z(W)$是对信道可靠性的衡量，$Z(W)$越大，相应对称容量$I(W)$越小，说明该信道越不可靠。

对于其他信道，如二进制输入对称信道（Binary-input Symmeric Channel，BSC）或者二进制输入加性高斯白噪声信道（Binary-input Additive White Gaussian Channel，BAWGNC）并不存在准确的能够计算$Z(W_N^{(i)})$的方法。Mori等人提出了密度进化（Density Evolution，DE）的构造方法，该方法适用于所有类型的B-DMC。在信道编码的传输信道模型均为BAWGNC信道下，也可使用高斯近似（Gaussian Approximation，GA）法对DE简化计算。

  • 由上文分析可知，在极化过程$\left(W_N^{(i)}, W_N^{(i)}\right) \rightarrow\left(W_{2 N}^{(2 i-1)}, W_{2 N}^{(2 i)}\right)$中，
  • \[\begin{aligned} & Z\left(W_{2 N}^{(2 i-1)}\right) \leq 2 Z\left(W_N^{(i)}\right)-\left[Z\left(W_N^{(i)}\right)\right]^2 \\ & Z\left(W_{2 N}^{(2 i)}\right)=\left[Z\left(W_N^{(i)}\right)\right]^2 \end{aligned}\]

其中不等式在当且仅当$W_N^{(i)}$是二进制删除信道（BEC）时成立。

在讨论信道极化时，研究的是二进制离散无记忆信道（B-DMC），而在构造极化码时使用的巴氏参数Z(W)想要取等使用的适用范围是二进制删除信道（BEC）。BEC是B-DMC的子集。

  N =8;
  ZW =0.5; %初始信道的巴氏参数
  ZW8 = ZW_cal(N, ZW);
  ZW8 = bitrevorder(ZW8); %按位置二进制比特翻转
  
  function ZWi = ZW_cal(N, ZW)
  ZWi = zeros(N, 1);
  ZWi(1) = ZW;
  m = 1; %极化级数
  while(m < N) 
      for j = 1 : m
          %计算信道极化
          Z_tmp = ZWi(j);
          % 根据文章中公式计算ZWi
          ZWi(j) = 2 * Z_tmp - Z_tmp * Z_tmp; %好信道
          ZWi(j + m) = Z_tmp * Z_tmp; %差信道
      end
  m = m * 2;
  end
  end

比特混合

选择可靠性最大的K个分裂子信道传输消息比特，其他分裂子信道传输冻结比特。这一步的输出即为编码的原始比特。

对于BEC信道来说，即选择巴氏参数最小的K个子信道放置消息比特。

生成矩阵

由数学推导得到以下结果，编码器递归构造（生成矩阵）表示为：$G_N=B_N F^{\otimes n}$

\[B_N=R_N(I_2 \otimes B_{N / 2})\]

其中$F^{\otimes n}$表示对$F$的n次克罗内克积。

\[F=\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right] ,A \otimes B=\left[\begin{array}{cccc} a_{11} B & a_{12} B & \cdots & a_{1 N} B \\ a_{21} B & a_{22} B & \cdots & a_{2 N} B \\ \vdots & \vdots & \ddots & \vdots \\ a_{N 1} B & a_{N 2} B & \cdots & a_{N N} B \end{array}\right]\\\] \[B_2=I_2\]

$I_n$为n阶单位矩阵

$B_N$为一个比特翻转矩阵，$R_N$是一个排列运算，即实现技奇数位放在前面，偶数位在后面。如

\[\left[\begin{array}{l} 1 & 3 & 2 & 4 \end{array}\right]= \left[\begin{array}{l} 1 & 2 & 3 & 4 \end{array}\right]R_4 \quad , R_4=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\]

编码举例

假设对于各BEC信道，已计算出各个分裂信道的巴氏参数。根据信道容量排序，假设子信道序号为”4，6，7，8“的巴士参数最小，因此将休眠比特放在{1,2,3,5}的位置 ，信息比特放于{4,6,7,8}位置。假设休眠比特为0，信息比特为(1,1,1,1)。最终得到

\[u^8=[0,0,0,1,0,1,1,1]\]
  • 求排序矩阵BN

由递归式，

\[B_8=R_8\left(I_2 \otimes B_4\right) \\ B_4=R_4\left(I_2 \otimes B_2\right) \\\]

因此可求

\[B_2=I_2=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \quad , I_2 \otimes B_2=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] \[R_4=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \quad , R_8=\left[\begin{array}{llllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right]\] \[\therefore B_4=R_4\left(I_2 \otimes B_2\right)=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \cdot\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\] \[I_2 \otimes B_4=\left[\begin{array}{llllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right]\] \[\therefore B_8=R_8(I_2 \otimes B_4)=\left[\begin{array}{llllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right]\]
  • 求F的n次克罗内克积
\[\begin{aligned} & F^{\otimes 1}=F=\left[\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right] \\ & F^{\otimes 2}=F \otimes F^{\otimes 1}=\left[\begin{array}{cc} F & 0 \\ F & F \end{array}\right]=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] \\ & F^{\otimes 3}=F \otimes F\otimes F=F \otimes F^{\otimes 2}=\left[\begin{array}{ccc} F^{\otimes 2} & 0 \\ F^{\otimes 2} & F^{\otimes 2} \end{array}\right]=\left[\begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{array}\right] \\ & \end{aligned}\]
  • 计算生成矩阵
\[G_8=B_8 F^{\otimes 3}=\left[\begin{array}{llllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{array}\right]\]
  • 生成polar码
\[\begin{aligned} x^8 & =u_1^8 G_8=\left[\begin{array}{llllllll} 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \end{array}\right] \cdot\left[\begin{array}{llllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{array}\right] \\ & =\left[\begin{array}{llllllll} 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{array}\right] \end{aligned}\]

  • MATLAB仿真

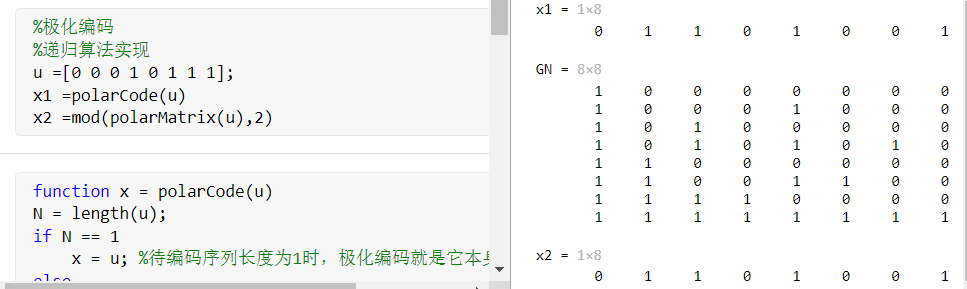
    这里使用上述一样的初始序列$u_1^8$，分别使用递归算法与矩阵运算实现编码，结果分别为$x_1,x_2$

%极化编码
%添加休眠比特后的码字
u =[0 0 0 1 0 1 1 1];

x1 =polarCode(u) %递归算法实现
x2 =polarMatrix(u) %矩阵运算实现编码

function x = polarCode(u)
N = length(u);
if N == 1
    x = u; %待编码序列长度为1时，极化编码就是它本身
else
    %将待编码序列u分为前半段、后半段
    %前半段与后半段进行模2加，结果存放于前半段中
    u1 = mod(u(1 : N/2) + u(N/2 + 1 : N) , 2);
    %后半段不变
    u2 = u(N/2 + 1 : N);
    %运行递归计算
    x = [polarCode(u1) polarCode(u2)];
end
end

function x = polarMatrix(u)
% u的长度需为2的幂次
N = length(u);
if N == 1
    x =u;
% 判断是否为2的幂次方长度，不足补零，在从结果中取前N位
elseif 2^nextpow2(N) ~= N
    tmp = zeros(1,2^nextpow2(N));
    tmp(1:N) = u;
    x =polarMatrix(tmp);
    x =x(1:N);
else
    n =log2(N);
    Gpre =1;
    %每一层递归都相当于计算一个新的生成矩阵
    for i=1:n
        %这个新的生成矩阵的维度为 Ni/2
        Ni = 2 ^ i;
        A = zeros(Ni);
        for j = 1 : Ni / 2
            A(2 * j - 1 , j) = 1;
            A(2 * j , j) = 1;
            A(2 * j , Ni / 2 + j) = 1;
        end
        G = A*kron(eye(2),Gpre);
        Gpre = G;
    end
    GN =G %生成矩阵GN
    x =mod(u *GN,2); 
    %GN与u的运算中加法代表异或运算，在矩阵相乘后使用模2实现异或结果
end
end

极化译码

最小单元译码

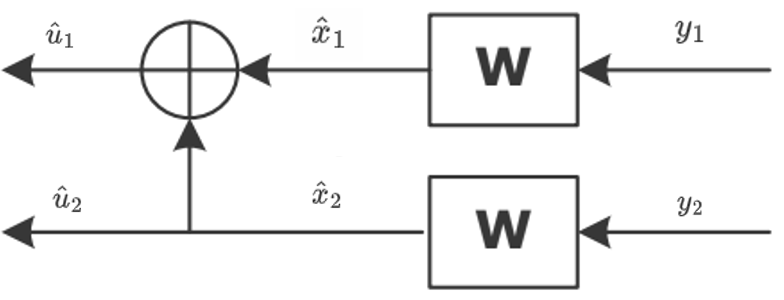
\[L R(\hat{\mathbf{u}}_1)=\frac{P(\hat{\mathbf{u}}_1=0)}{P(\hat{\mathbf{u}}_1=1)}=\frac{P(\hat{\mathbf{x}}_1=0) P(\hat{\mathbf{x}}_2=0)+P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=1)}{P(\hat{\mathbf{x}}_1=0) P(\hat{\mathbf{x}}_2=1)+P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=0)} \\=\frac{\frac{P(\hat{\mathbf{x}}_1=0) P(\hat{\mathbf{x}}_2=0)+P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=1)}{P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=1)}}{\frac{P(\hat{\mathbf{x}}_1=0) P(\hat{\mathbf{x}}_2=1)+P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=0)}{P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=1)}}\\ =\frac{1+L R(\hat{\mathbf{x}}_1) LR(\hat{\mathbf{x}}_2)}{LR(\hat{\mathbf{x}}_1)+L R(\hat{\mathbf{x}}_2)}\]

  • 如若$\hat u_1=0$，若使$\hat u_2=0$，则必须$\hat x_1=\hat x_2=0$；$\hat u_2=1$则$\hat x_1=\hat x_2=1$

    \[L R_{\hat{\mathbf{u}}_1=0}(\hat{\mathbf{u}}_2)=\frac{P_{\hat{\mathbf{u}}_1=0}(\hat{\mathbf{u}}_2=0)}{P_{\hat{\mathbf{u}}_1=0}(\hat{\mathbf{u}}_2=1)}=\frac{P(\hat{\mathbf{x}}_1=0) P(\hat{\mathbf{x}}_2=0)}{P(\hat{\mathbf{x}}_1=1) P(\hat{\mathbf{x}}_2=1)}=L R(\hat{\mathbf{x}}_1) L R(\hat{\mathbf{x}}_2)\]

    同理，可求得

    \[L R_{\hat{\mathbf{u}}_1=1}(\hat{\mathbf{u}}_2)=\frac{P_{\hat{\mathbf{u}}_1=1}(\hat{\mathbf{u}}_2=0)}{P_{\hat{\mathbf{u}}_1=1}(\hat{\mathbf{u}}_2=1)}=\frac{LR(\hat{\mathbf{x}}_2)}{LR(\hat{\mathbf{x}}_1)}\]

    即有$LR(\hat{\mathbf{u}}_2)=[LR(\hat{\mathbf{x}}_1)]^{1-2 \hat{\mathbf{u}}_1} LR(\hat{\mathbf{x}}_2)$

  • 实际使用中更多使用对数似然比（LLR），则有
  • \[LLR(\hat{\mathbf{u}}_1)=\ln \frac{1+e^{L_1+L_2}}{e^{L_1}+e^{L_2}} \approx \operatorname{sign}\left(L_1\right) \operatorname{sign}\left(L_2\right) \min \left\{\left|L_1\right|,\left|L_2\right|\right\}\\\]

其中$L_1,L_2$分别为接收信号的LLR，$sign$表示取符号位，上式常被称为$f$运算。得到$u_1$后即可进行$u_2$的译码，即有

\[LLR(\hat{\mathbf{u}}_2)=(1-2u_1)L_1+L_2\]

上式常被称为$g$运算。得到$LLR(\hat{\mathbf{u}}_1),LLR(\hat{\mathbf{u}}_1)$后即可进行判决，若$LLR\geq 0$判决为0，$LLR<0$判决为1。（同理$LR\geq 1$判决为0，反之判决为1）

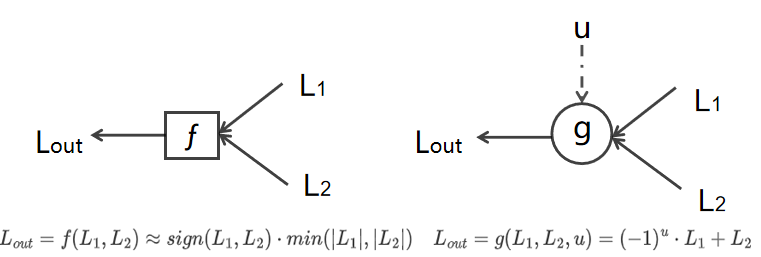
如果使用BPSK调制，$s=1-2x，s\in { 1,-1}$为发送BPSK信号，$y=s+n$是接收信号，其中$n$是均值为0，方差为$\sigma ^2$的高斯加性白噪声，则接收信号y的$LLR=\ln \frac{\frac{1}{\sigma \sqrt{2 \pi}} e^{-(y-1)^2 /\left(2 \sigma^2\right)}}{\frac{1}{\sigma \sqrt{2 \pi}} e^{-(y+1)^2 /\left(2 \sigma^2\right)}}=\frac{2}{\sigma^2} y$

串行抵消译码（SC译码）算法

SC :Successive Cancellation，串行抵消

  • 这里以一个例子来说明SC译码过程。配置如下（AWGN信道传输，$E_b/N_0=4dB$）：

    码长$N=8$，信息比特数$K=4$，码率$R=K/N=0.5$，信息比特集合${4,6,7,8}$，冻结比特全部取0,4个信息比特为$(1,1,1,1)$，则$\mathbf{u_1}^8=(00010111)$，$\mathbf{x_1}^8=\mathbf{u_1}^8F^{\otimes 3}=(01101001)$即编码后polar码（具体见极化码编码举例）。$\mathbf{x_1}^8$对应BPSK序列$\mathbf{x_1}^8=(1,-1,-1,1,-1,1,1,-1)$，生成随机噪声序列$\mathbf{n_1}^8=(-1.4,0.5,0.2,-0.8,-0.3,0.2,2.3,1.7)$，接收信号为$\mathbf{y_1}^8=\mathbf{s_1}^8+\mathbf{n_1}^8=(-0.4,-0.5,-0.8,0.2,-1.3,1.2,3.3,0.7)$，接收对数似然比为$\mathbf{L_1}^8=\frac{2}{\sigma^2}\mathbf{y_1}^8=(-2.0,-2.5,-4.0,1.0,-6.5,6.0,16.6,3.5)$。

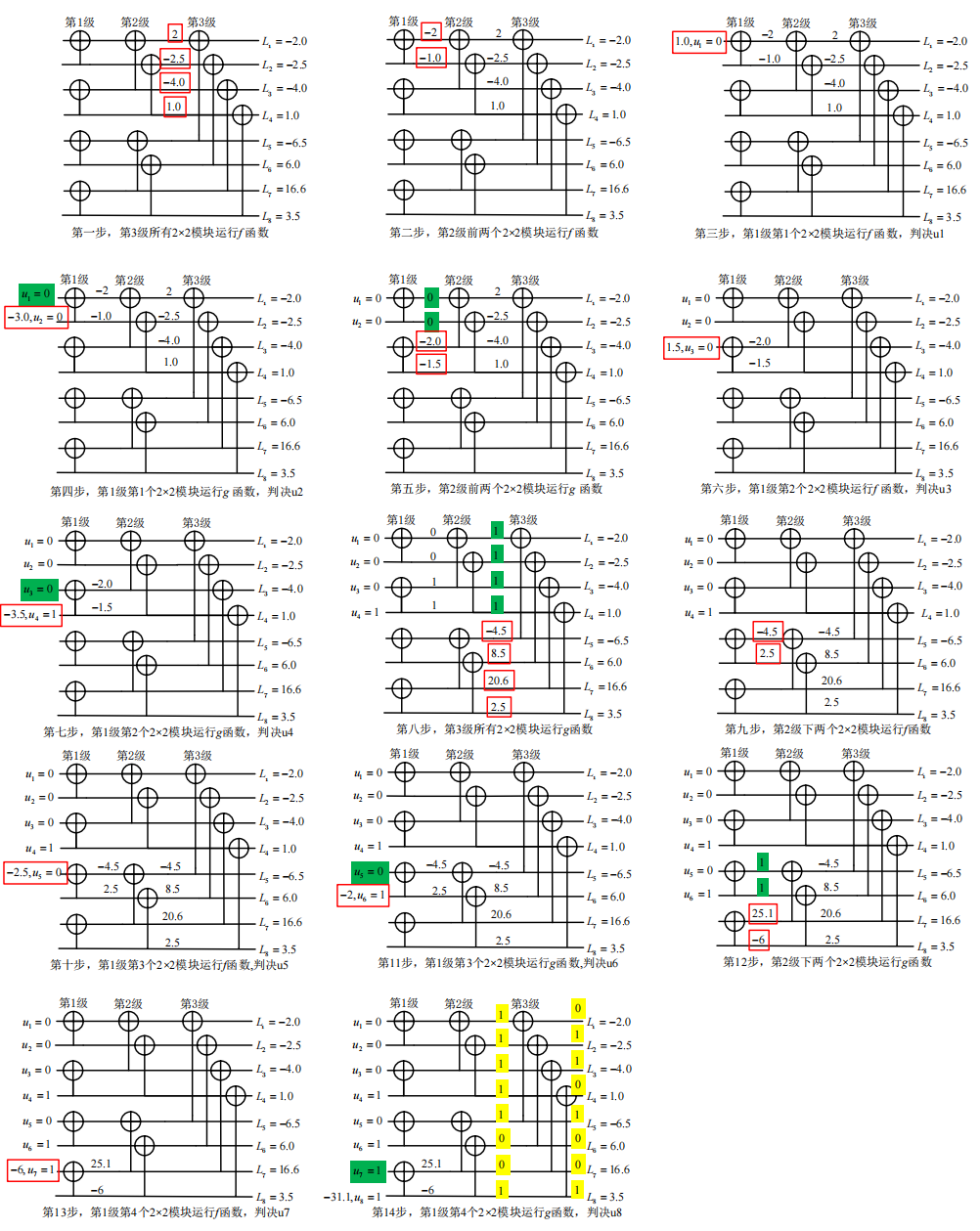
    上述译码可用二叉树表示，与编码图译码过程一致

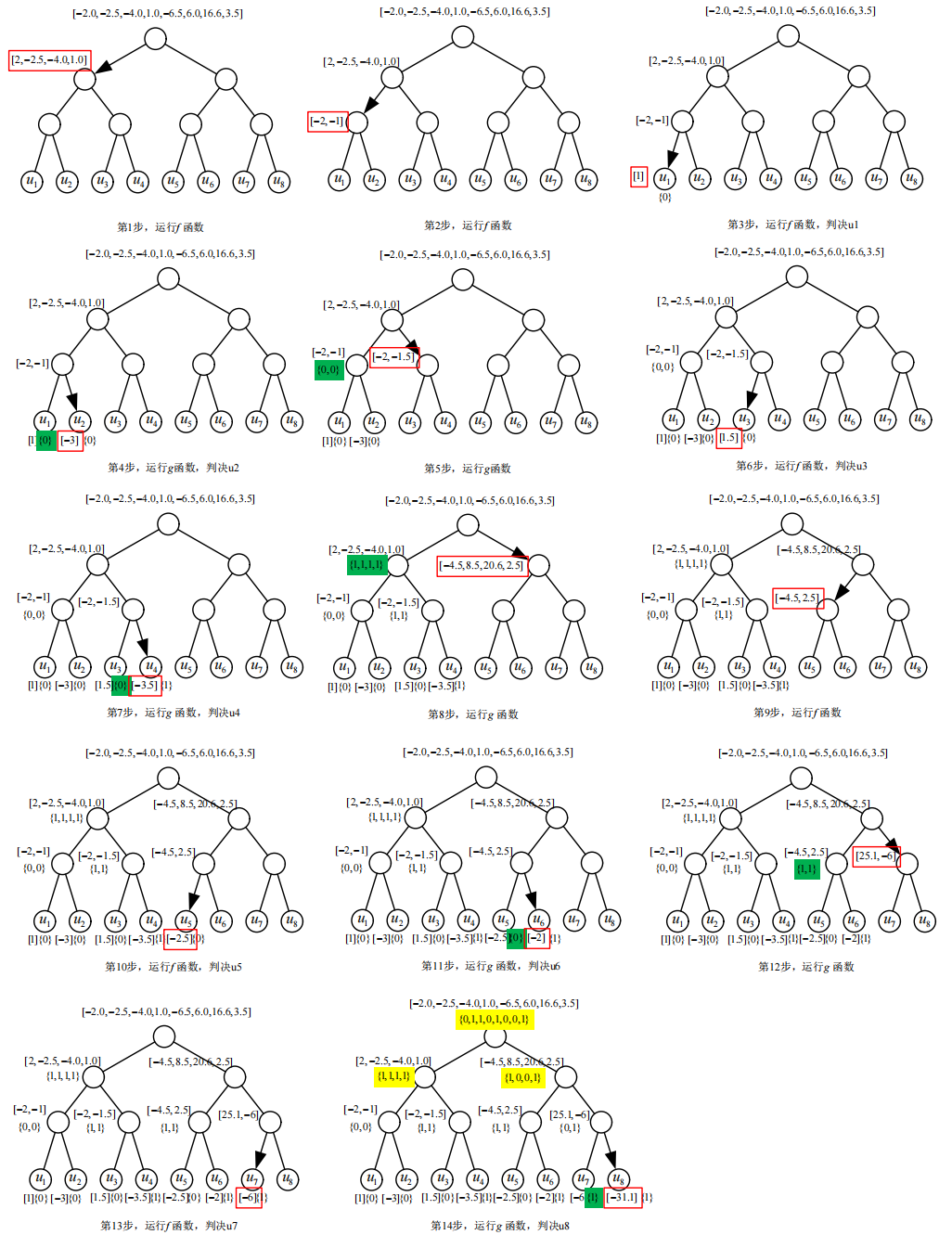
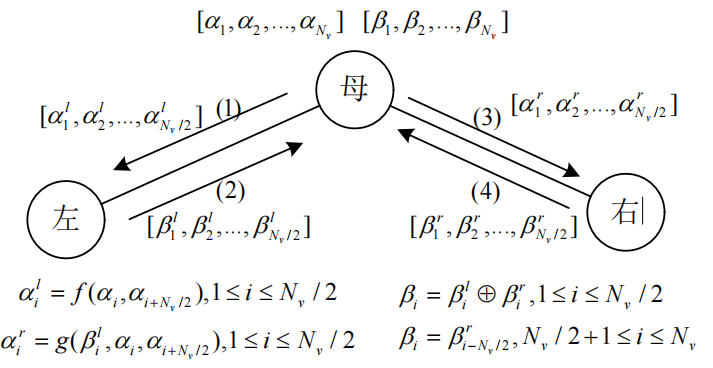
    下图即SC译码的二叉树每个节点一般规律：

    • 对任意一个母节点：
      • 将母节点长度为N的LLR序列进行N/2次f运算得到左子节点的LLR序列
      • 若左子节点非叶节点，以此为新的母节点向下递归。
      • 若左子节点为叶节点，如为休眠比特，直接判决为0；如为信息比特，通过LLR硬判决（大于等于0判0，小于0判1）。将判决结果传回母节点。
      • 通过得到的部分判决结果与LLR序列进行N/2次g运算得到右节点LLR序列。
      • 同左子节点操作。母节点得到左右子节点判决结果后进行运算得到母节点所对应判决结果。
    • 递归实现整个二叉树的译码。

  • MATLAB仿真实现SC译码（LLR与上例相同）

    %极化译码
% 对数似然比
LLR =[-2.0 -2.5 -4.0 1.0 -6.5 6.0 16.6 3.5];
% 冻结比特位（1是冻结位）
frozen_bits =[1 1 1 0 1 0 0 0];
[u, b] = SC_decode(LLR, frozen_bits)
  
function [u, b] = SC_decode(llr, frozen_bits)
N = length(llr);
if N == 1
    if frozen_bits
        u = 0; 
    else
        u = llr < 0; %应硬判决；小于0判决为1，大于等于0判决为0
    end
        b = u;
else
    %运行f运算
    alpha_left = f(llr(1 : N/2), llr(N/2 + 1 : N)); 
    %递归译码
    [ u_left_child, beta_left_child ] = SC_decode(alpha_left, frozen_bits(1 : N/2)); 
    %运行g运算
    alpha_right = g(beta_left_child, llr(1 : N/2), llr(N/2 + 1 : N)); 
    %递归译码
    [ u_right_child, beta_right_child ] = SC_decode(alpha_right, frozen_bits(N/2 + 1 : N));
    %合并译码结果
    u = [ u_left_child u_right_child]; 
    b = zeros(1, N);
    b(1 : N/2) = mod(beta_left_child + beta_right_child, 2);
    b(N/2 + 1 : N) = beta_right_child;
end
end
  
function [z] = f (x , y)%f函数
    z = sign(x) .* sign(y) .* min(abs(x), abs(y));
end
  
function [z] = g(u, x, y)%g函数
    z = (1 - 2 * u ) .* x + y;
end

SCL译码算法

  • Polar Code在码长趋于无穷时，信道极化才越完全。但在有限码长下，由于信道极化并不完全，依然会存在一些信息比特无法被正确译码。由前面的译码流程可知，SC译码器在对后面的信息比特译码时需要用到之前的信息比特的估计值，如果前面的信息比特的译码中发生错误，就会产生错误传递且无法对错误进行修改。

  • 针对以上缺点，SCL算法，即串行抵消列表算法，增加了列表这一元素，即增加每一层路径搜索后允许保留的候选路径数量，每一层扩展后，尽可能多地保留后继路径（每一层保留的路径数不大于L）。完成一层的路径扩展后，选择路径度量值（Path Metrics，PM）最小的L条，保存在一个列表中，等待进行下一层的扩展。

  • 定义路径度量值（PM） 路径度量即某个译码结果的后验概率 $\operatorname{Pr}(\mathbf{u}_1^i |\mathbf{y}_1^N)$

    该值越大说明$u_1^i$的正确概率越大，使用$u_1^i$后续译码$u_{i+1},\dots u_N$，最终译码正确率也就越大。经数学验证可知有如下公式：

    \[-\ln \operatorname{Pr}\left(\mathbf{u}_1^i \mid \mathbf{y}_1^N\right)=\sum_{k=1}^i \ln \left(1+\mathrm{e}^{-\left(1-2 u_k\right) L_N^{(k)}}\right)\]

    令$PM=-\ln \operatorname{Pr}(\mathbf{u}_1^i \mid \mathbf{y}_1^N)$则PM越小，译码正确率越高。

    为何不直接使用LLR相加进行路径度量？

  • 算法流程：

    （1）SCL译码器内部并行放置L个SC译码器，记作$SC_1,SC_2,\dots ,SC_N$

    （2）SCL姨妈期获得接收对数似然比序列$(L_1,L_2,\dots,L_N)$，初始化路径度量0，激活1号译码器，未激活译码器为$S_{sleep}={2,3,\dots,L}$。

    （3）激活的1号译码器进行标准SC译码，计算出$L_N^{1}$（1号比特位对数似然比）。判断该位是否为冻结比特位。若为冻结比特直接令$u_1=0$；若为信息比特，判断SCL未激活译码器$S_{sleep}$是否有剩余，若有则从$S_{sleep}$中弹出一个译码器并继承此时1号译码器的全部数据。令原始译码路径（这里为$S_1$）的$u_1=0$，克隆路径的$u_1=1$。分别计算路径度量值，并开始译码下一个比特。

    \[\begin{aligned} & \operatorname{Pr}\left(\mathbf{u}_{1,1}^i \mid \mathbf{y}_1^N\right)=\sum_{k=1}^{i-1} \ln \left(1+\mathrm{e}^{-\left(1-2 u_{k, 1}\right) L_N^{(k)}}\right)+\ln \left(1+\mathrm{e}^{-L_N^{(i)}}\right) \\ & \operatorname{Pr}\left(\mathbf{u}_{1, 2}^i \mid \mathbf{y}_1^N\right)=\sum_{k=1}^{i-1} \ln \left(1+\mathrm{e}^{-\left(1-2 u_{k, 2}\right) L_N^{(k)}}\right)+\ln \left(1+\mathrm{e}^{L_N^{(i)}}\right) \end{aligned}\]

    即SCL译码器同时保留了$u_i=0,1$两种译码结果。

    （4）激活的不同译码器继续使用各自的数据独立译码，即运行（3）步（把(3)中1号译码器换为当前译码的i号译码器，$u_1$变为$u_i$）

    （5）上述过程持续，直至$S_{sleep}=\varnothing$，记此时译码的信息比特为$u_t$，此时所有L个已激活译码器各自有判决$u_t$的$PM_l,LLR:L_{N,l}^t\quad ,1\leq l\leq L$。取$u_t=0,1$两种结果，计算得2L个路径度量，SCL译码器将从下面2L个译码结果中选取L个最小路径度量值的译码结果保留。

    \[\mathbf{P M}=\left[\begin{array}{ccccc} P M_1+\ln \left(1+\mathrm{e}^{-L_{N, 1}^{(t)}}\right) & \ldots & P M_l+\ln \left(1+\mathrm{e}^{-L_{N, l}^{(t)}}\right) & \ldots & P M_L+\ln \left(1+\mathrm{e}^{-L_{N, L}^{(t)}}\right) \\ P M_1+\ln \left(1+\mathrm{e}^{L_{N, 1}^{(t)}}\right) & \ldots & P M_l+\ln \left(1+\mathrm{e}^{L_{N, l}^{(t)}}\right) & \ldots & P M_L+\ln \left(1+\mathrm{e}^{L_{N, L}^{(t)}}\right) \end{array}\right]\]

    PM中第$l$列表示译码器$SC_l$，第一行表示每个译码器对$u_t$译0的结果，第二行表示译1。

    对PM中每列共存在3中情况：

    1、该列中两个元素均未选入L个最小值，此时$SC_l$休眠并回收入$S_{sleep}$。

    2、该列仅一个元素选入L个最小值，此时$SC_l$译码器保留选入的对应比特，并按（3）中公式更新路径度量。

    3、该列两个元素均选入L个最小值。易知，一旦该情况出现，情况1必然存在，否则幸存路径多于L个。此时保留判决$u_{t,l}=0$，并更新路径度量。随后从$S_{sleep}$中弹出一个译码器并继承$SC_l$的全部数据，令该译码器$u_{t,k}=1$，并据此更新路径度量。

    （6）$u_t$后译码若为休眠比特直接判0并更新路径度量PM，若为信息比特进行（6）。以此重复直至N个译码结束。

    （7）选择L个译码器中路径度量最小的最为SCL译码器输出。

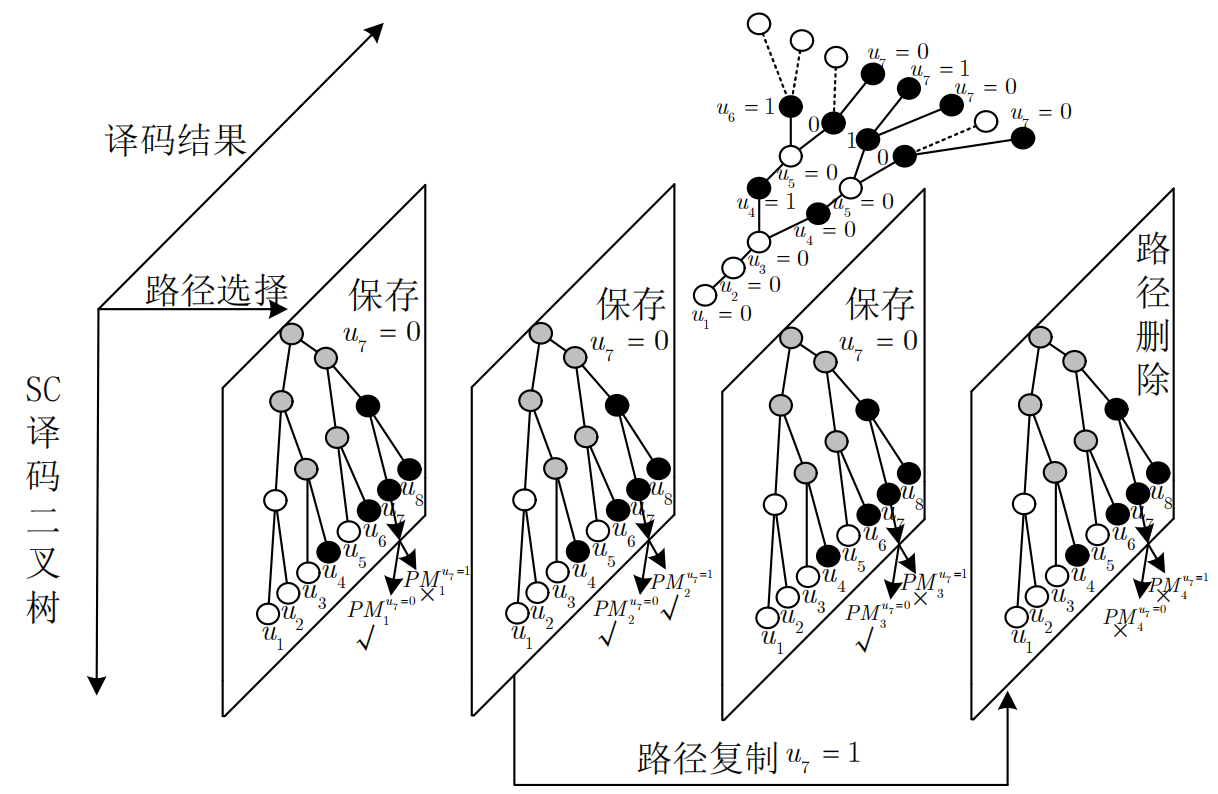
  • 从上述译码流程中记参数L为搜索宽度。当L=1时，SCL译码算法退化为SC译码算法；当$L\geq2^K$（K为信息比特数）时，SCL译码等价于最大似然译码。可以看出SC译码算法是深度优先的，要的是从根节点快速到达叶子节点。而SCL译码算法是广度优先的，先扩展，再剪枝，最终到达叶子节点。

总结

  • Polar 码是一种新近提出的基于信道极化这一数字信号处理技术的纠错编码方法，本文对信道极化现象和 Polar 码的编码、译码原理进行了研究。

    现在，分析一下 Polar 码的优势与主要问题。优势：1、已在实际系统中被广泛应用的一些其它信道编码方案，如 Turbo 码、LDPC 码等，在码长接近无限长时能够非常逼近容量，但始终不能或至少无法被证明能够达到容量；而 Polar 码在码长趋于无穷的场景下能够被严格证明容量可达；2、具有明确的构码方法；3、编译码复杂度相对较低，获得接近最大似然解码性能；4、采用合适的译码方法其性能可超越最好的 LDPC码与 Turbo 码。

    主要缺点有：

    1、最小汉明距离较小，可能在一定程度上影响解码性能。

    2、SC 译码的时延较长，采用并行解码的方法则可以缓解此问题。

    Polar 码较好地平衡了性能和复杂性，在中短码长的情形下比较有优势。总之，极化编码理论在实际通信系统中可以有很广阔的应用前景，存在着大量值得研究的应用问题，如信源编码、多用户通信、物理层保密通信等。这些问题中的一部分己经得到了一些学者的关注，但即使是这部分问题，对其的研究大多数也依然仅仅停留在理论阶段，为了在未来的通信系统中进行实际地部署、应用，仍然需要大量的研究工作。

参考文档

[1] Erdal Arikan. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Transactions on information Theory, 55(7):3051–3073,2009.

[2] 于永润. 极化码讲义

[3] Polar Code 24节

[4] 不错的PPT